どうも京大生時代に塾講師を6年間していたMANUです!
この記事では、
「京大数学はパターンだけで解けるのか?」
という受験生が必ず抱く疑問に、京大史上最も有名で良問の1つ「tan1°は有理数か?」という問題を使って考察していこうと思います。
今回の記事は、数学全般に役立つ内容になっていますので、数学を得意教科にしたい人はぜひ読んで見てください!!
・数学はパターンで解けるのか興味がある人
・京大数学に興味がある人
・数学を得意教科にしたい人
・難関大を目指す高校生
それではさっそくLet’s get started !!
問題の説明
ちょっとした裏話
今回紹介する京大理系数学の問題は実はあることで有名になりました。
tan1°は有理数か。
それは大学入試史上最も短い問題文ということ。
tan1°を、仮に1文字としてカウントするとたったの7文字になります。
実はこの入試問題が出題させる数年前に、東京大学で
「円周率が3.05より大きいことを証明せよ。」
という超シンプルな問題(文字数18)が出て、話題になったんですが、これに対抗する形で京都大学もさらに超シンプルな問題を出したんではないかと噂されています。
東京大学と京都大学は、互いに日本で一番質の高い問題を作ろうといつも切磋琢磨しているので、比較してみると結構似てる部分があったり面白いですよ。
難易度及び解答・解説
ちなみにこの問題は受験生のほとんどが解けなかったそうです。
これから紹介する解答を紹介すると意外とあっさりしているんですが、多くの受験生がこの問題の「ある落とし穴」にはまってしまったようです。
それでは簡単な解答・解説から。

【解答・解説】
「tan1°は有理数か」という問いに対して、いきなり答えるのは難しいので、他の有名角のtanを考えてみましょう。
例えば
tan30°=1/√3 ⇒ 無理数
tan45°=1 ⇒ 有理数
tan60°=√3 ⇒ 無理数
こんな感じで有名角のtanの値すら無理数が多いですよね。
三角関数の値が有理数になる場合は特殊なケースで、ほぼ無理数になることはある程度三角関数を触ったことがある人なら分かるはず。
したがってtan1°は無理数である可能性が高いという仮説が立ちます。
無理数であることを示すには
「有理数であると仮定して、矛盾を示す(背理法)」
というのが王道中の王道。
tan1°=n/m(有理数)と置き、矛盾を示します。
さてここから、tan1°(有理数と仮定)と無理数を結びつけていきます。
無理数はtan60°=√3が使いやすそうですね。
tan1°を使ってtan60°を表現しようと考えます。
tanの式変形に使える道具は、加法定理です。
加法定例から、tan(1°+1°)を考えるとtan2°は有理数になりますよね。
更に言うとtan(1°+2°)=tan3°も有理数になります。
したがって帰納的に、tan4°, tan5°,… ,tan60°も有理数になりますね。
しかしtan60°=√3で無理数ですから矛盾となり、背理法よりtan1°が無理数であることが証明完了です。
問題の考察
受験生がハマった落とし穴
この問題の解答を見ると、
「tan1°を有理数と仮定(背理法)⇒加法定理を利用して矛盾を指摘」
というシンプルなものになっています。
背理法も加法定理も高校2年生ならみんなが知っている有名な解法手法です。
なぜ解法自体はシンプルなのに、受験生は解けなかったのか。それは、
背理法を使うことすら気付かなかったから
「tan1°は有理数か」
と聞かれて
「確かにtan1°は有理数かもしれない。有理数であることを証明しよう!」
「そもそも有理数と無理数ってどうやって判定するんだっけ?」
こんな感じで愚直に考えてしまう生徒が多いです。

これでは京都大学が用意した罠にはまってます。
tan1°は有理数じゃないし、有理数か無理数を判定するような便利な公式もこの世にはありません。
京都大学の先生たちは、次のステップでこの問題を解いてほしいと思っているはずです。
- tan1°が有理数か無理数か、これまでの知識を総動員して冷静に見定める
- 無理数の方が可能性が高そうだと気付く。
- そして無理数であることを背理法を使って示す。
- 以下は加法定理をうまく使って解答完了。
多くの受験生はステップ①、②が出来なかったんです。
なぜなら①、②の作業はパターン通りじゃないから。
パターン通りの③、④の作業にたどり着くまえに、パターン通りじゃない思考を必要とするのが京都大学の特徴なんです。
おそらく他の大学なら、今回の問題はこのように出したと思います。
tan1°は無理数であることを証明せよ
あらかじめ、tan1°は無理数であることを教えてあげたうえで、パターン通りに解けるかを試すと思われます。
京大数学は単純なパターンじゃない
京都大学の数学はこの問題に代表されるように、
パターン通りに解ける解法にたどり着くまでに、パターン通りじゃない思考をさせる
という特徴があります。
問題を見た瞬間に、
「あのパターンを使えば解ける!!」
ってなるのはほぼ京大数学の場合ありません。
「自分の知ってる解法パターンにどのように結び付けるか。」という思考力を問うのが京大数学の特徴です。
イメージにするとこんな感じ。
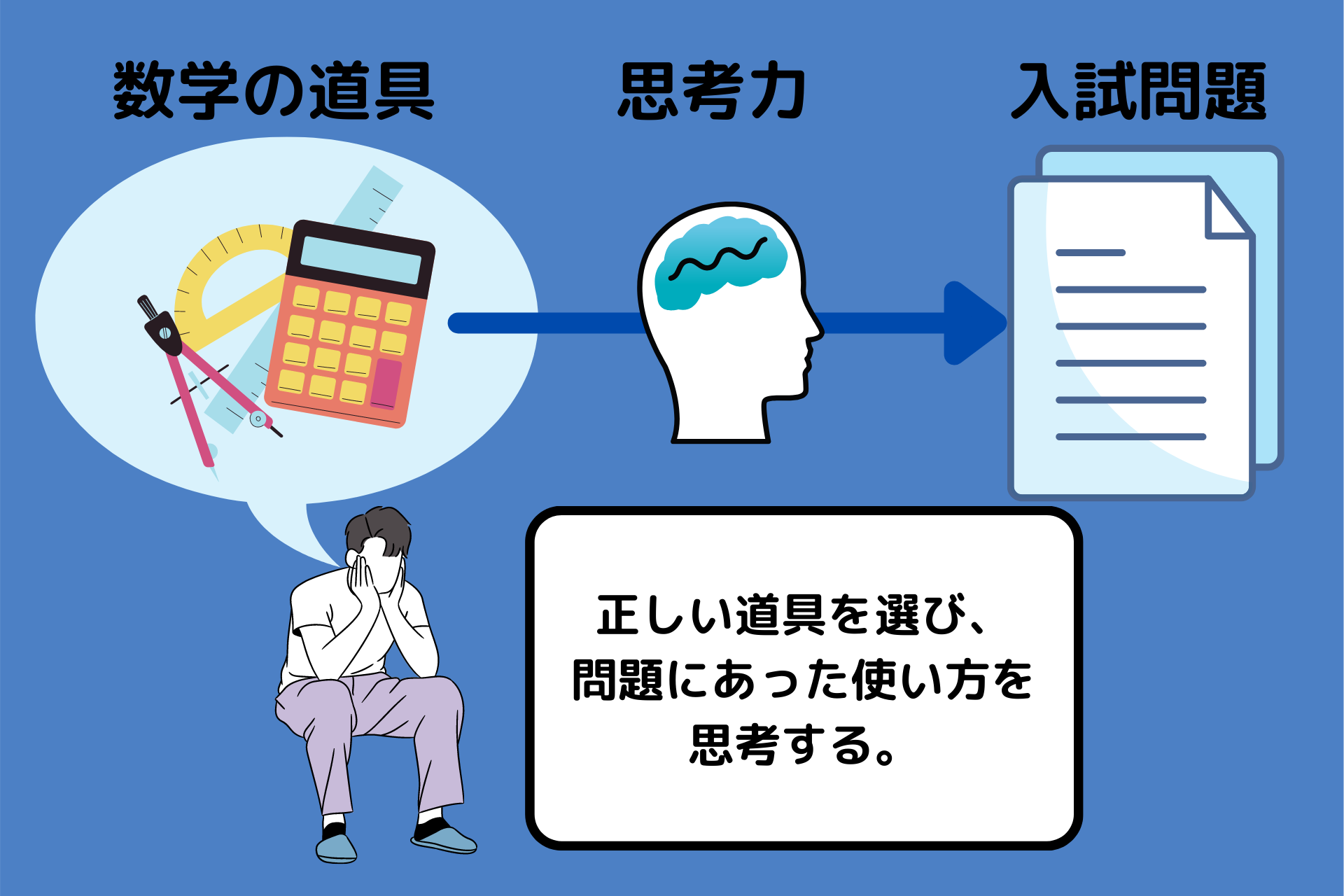
受験生は、この図でいう思考力を鍛える必要があります。
つまり京都大学の数学は「数学の道具」をため込むだけで解けてしまうほど、簡単ではありません。(単純なパターンじゃない。)
京大数学は数学の道具と入試問題の距離が遠いため、「思考力」を使って、適切な道具を選んであげる必要があります。
この感覚がつかめるようになると京都大学の数学は一気に解けるようになると思います。
最後に
皆さんいかがでしょうか。
今日は最も有名な京都大学の数学の問題を使って、
「京都大学の数学はパターン通りに解けるのか」
という命題を考察してみました。
まとめるとこんな感じ!
- 解法自体はパターン通りに解ける
- 適切な解法を選ぶのにパターンじゃない思考力が必要
今回の記事が皆様の学力向上に一役買えれば嬉しい限りです。
今日も記事を読んでくれてありがとうございました。












